Data Structures — A Quick Comparison (Part 2) 数据结构2-快速比较
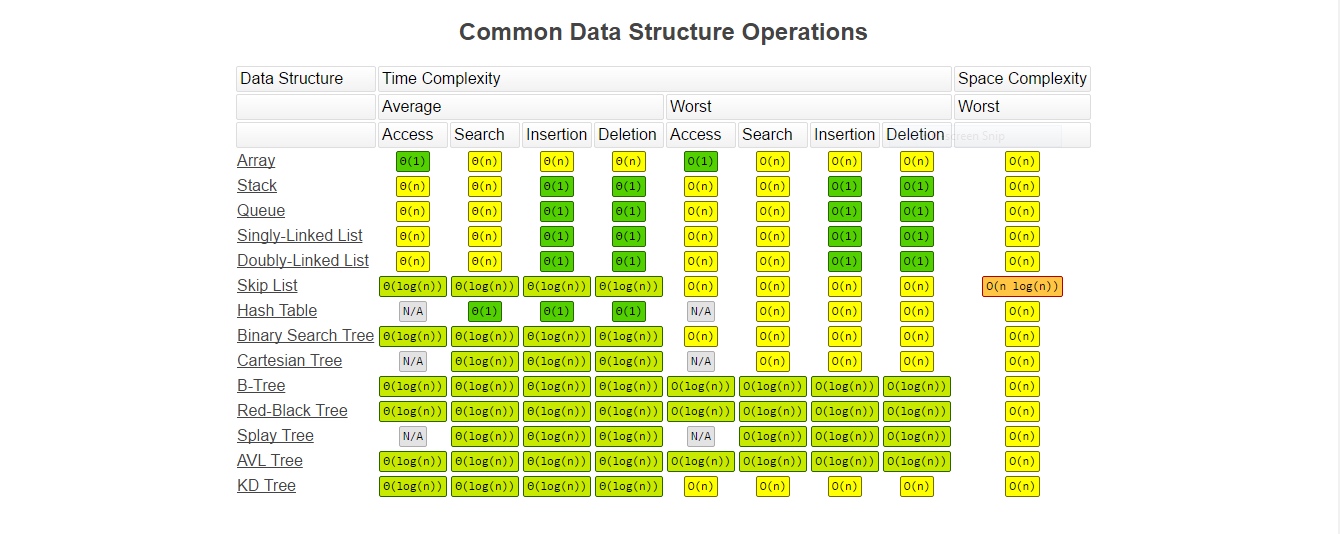
Comparison between different data structures — bigocheatsheet.com 不同数据结构之间的比较——bigocheatsheet.com
Each data structure has it’s own different way, or different algorithm for sorting, inserting, finding, …etc. This is due to the nature of the data structure. There are algorithms used with specific data structure, where some other can’t be used. 每个数据结构都有自己不同的排序、插入、查找等方法或算法。这是由于数据结构的性质。有些算法具有特定的数据结构,而其他一些算法不能使用。
The more efficient & suitable the algorithm, the more you will have an optimized data structure. 算法越高效、越合适,就越能得到优化的数据结构。
Chances are, you’re going to rely on the built-in algorithms used with the data structures in your language. These algorithms are very well optimized and battle tested. 很可能,您将依赖于与您的语言中的数据结构一起使用的内置算法。这些算法都经过了很好的优化和测试。
arrays 数组
pros 优点
-
Easy to create, Easy to use 易于创建,易于使用
-
Direct indexing: O(1) 直接索引:O(1)
-
Sequential access: O(N) 顺序存取:O (N)
cons 缺点
-
Sorting: O(NLogN) 排序:O(NLogN)
-
Searching: O(N), and O(LogN) if sorted 搜索:O(N)和O(LogN)如果排序
-
Inserting and deleting: O(N) because of shifting items. 插入和删除:O(N)由于移动项目。
linked list 链表
pros 优点
-
Inserting and deleting: O(1). 插入和删除:O(1)
-
Sequential Access: O(N) 顺序存取:O(N)
Inserting and deleting operations refers to the operation itself, as you might need to sequentially access all the nodes until the node you’are looking for. 插入和删除操作指的是操作本身,因为您可能需要顺序访问所有节点,直到您要查找的节点。
Inserting and deleting is much easier with doubly linked list. 使用双链表插入和删除要容易得多。
cons 缺点
-
No Direct Access; Only Sequential Access. 没有直接访问;只有顺序存取
-
Searching: O(N) 搜索:O (N)
-
Sorting: O(NLogN) 排序:O(NLogN)
Stacks and Queues 栈和队列
Stacks and queues have very specific purposes. Stacks are last in, first out data structure (LIFO), while queues are first in, first out (FIFO). 堆栈和队列有非常特定的用途。栈是后进先出的数据结构(LIFO),而队列是先入先出(FIFO)。
pros 优点
- Push/Add: O(1)
- Pop/Remove: O(1)
- Peek: O(1)
Cons
If you’re trying to do anything else with stacks or queues, like if you’re asking how can I pull an item from the middle?. Then, you should be looking at a different data structure. 如果您想对堆栈或队列做其他任何事情,比如如果您想知道如何从中间提取项目?然后,您应该查看不同的数据结构。
Hash Tables. 哈希表
pros 优点
-
Inserting and deleting: O(1) + Hashing & Indexing (amortized). 插入和删除:O(1) +哈希和索引(平摊)。
-
Direct access: O(1) + Hashing & Indexing. 直接访问:O(1) +散列和索引。
It takes a little processing for the hashing and indexing. But the good thing about that is it’s the same amount of processing every time, even if the hash table gets very large.散列和索引需要一些处理。但是这样做的好处是每次处理的数量是相同的,即使哈希表变得非常大。
When the hash table gets full, it will increase it’s size. And, when the number of filled buckets is much smaller than the size of the hash table, it will then decrease it’s size. Both operations take a complexity of O(N). That’s why insertion and deletion takes O(1) amortized. 当哈希表被填满时,它会增加它的大小。当填充桶的数量远远小于哈希表的大小时,它就会减小它的大小。这两种操作的复杂度都是O(N)。这就是为什么插入和删除需要O(1)平摊。
cons 缺点
-
Some overhead as require a little more space in memory than arrays. 一些开销比数组需要更多的内存空间。
-
Retrieval of elements doesn’t guarantee a specific order. 元素的检索不能保证特定的顺序。
-
Searching for a value (without knowing it’s key). 搜索一个值(不知道它是键)。
sets 集
pros. 优点
-
Checking membership; value existence. 检查会员;价值的存在。
-
Avoids duplicates 避免重复
The complexity of checking if a value contained in the set depends on the underlying data structure used to implemented the set.检查集合中是否包含值的复杂性取决于用于实现集合的底层数据结构。
In C++, It uses a binary search tree (probably a red black tree; a type of self balancing binary search tree). So, the complexity would be O(LogN), and O(N) if the tree is unbalanced.在c++中,它使用二叉搜索树(可能是红黑树;一种自我平衡的二叉搜索树)。复杂度是O(LogN)如果树是不平衡的,复杂度是O(N)
In Java, HashSet class implements the Set Interface using the hash table data structure. So, the complexity would be same as the hash tables(see above). 在Java中,HashSet类使用哈希表数据结构实现Set接口。因此,复杂度将与哈希表相同(参见上文)。
Cons
Sets are intentionally limited. There aren’t much you can do with them. So, they’re are terrible at almost everything else. 集合是有意限制的。你对它们无能为力。所以,他们几乎在其他方面都很糟糕。
Binary Search Trees (BST)
Pros
- Inserting and deleting
- Speed of Access
- Maintains sorted order; retrieval of elements is in order.
The complexity of insertion, deletion, and accessing would be O(LogN), and O(N) if the tree is unbalanced.插入、删除和访问的复杂性为O(LogN),如果树是不平衡的,则为O(N)。
Cons
- Some overhead because of their creation and management.一些开销是因为它们的创建和管理。
Heaps
Heaps are a type of binary tree that are great for priority queues.堆是一种非常适合优先级队列的二叉树类型。
Pros
- Find Min/Find Max: O(1)
- Inserting: O(LogN)
- Delete Min/Delete Max: O(LogN)
Cons
- Searching and deleting: O(N)
In searching and deleting, we will have to scan all the elements as they don’t guarantee a specific order, unlike BST.在搜索和删除时,我们必须扫描所有的元素,因为它们不能保证一个特定的顺序,不像BST。
Deleting requires to traverse the whole tree to access the element first, then delete it, where the deletion operation itself requires O(LogN).删除需要遍历整个树来访问元素,然后删除它,删除操作本身需要O(LogN)。
原文:https://medium.com/omarelgabrys-blog/data-structures-a-quick-comparison-6689d725b3b0