ARTS是
由左耳朵耗子--陈皓发起的一个活动: 每周至少做一个leetcode的算法题、阅读并点评至少一篇英文技术文章、学习至少一个技术技巧、分享一篇有观点和思考的文章。（也就是Algorithm、Review、Tip、Share简称ARTS），至少坚持一年。
ARTS 015
这是第15篇
Algorihm 算法题
本周做的算法题是二叉树的前序遍历、中序遍历、后序遍历。每种遍历分别用递归(recursive)和迭代(iteratively)实现。 三种遍历的递归实现基本是一样的，但是三种遍历的迭代实现是不一样的，其中后序遍历的迭代实现最难。
递归和迭代的不同： 递归: 程序调用自身的编程技巧称为递归 迭代: 利用变量的原值推算出变量的一个新值，迭代就是A不停的调用B.
电影故事例证： 迭代——《明日边缘》 递归——《盗梦空间》
参见：
https://blog.csdn.net/laoyang360/article/details/7855860
Google：递归 迭代
斐波那契数列为:0,1,1,2,3,5...
//迭代实现斐波那契数列
long fab_iteration(int index)
{
if(index == 1 || index == 2)
{
return 1;
}
else
{
long f1 = 1L;
long f2 = 1L;
long f3 = 0;
for(int i = 0; i < index-2; i++)
{
f3 = f1 + f2; //利用变量的原值推算出变量的一个新值
f1 = f2;
f2 = f3;
}
return f3;
}
}
//递归实现斐波那契数列
long fab_recursion(int index)
{
if(index == 1 || index == 2)
{
return 1;
}
else
{
return fab_recursion(index-1)+fab_recursion(index-2); //递归求值
}
}
前序遍历：根结点 —> 左子树 —> 右子树 中序遍历：左子树—> 根结点 —> 右子树 后序遍历：左子树 —> 右子树 —> 根结点
94. Binary Tree Inorder Traversal
Difficulty: Medium
Given a binary tree, return the inorder traversal of its nodes’ values.
Example:
**Input:** [1,null,2,3]
1
\
2
/
3
**Output:** [1,3,2]```
**Follow up:** Recursive solution is trivial, could you do it iteratively?
#### Solution
Language: **C**
```c
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Return an array of size *returnSize.
* Note: The returned array must be malloced, assume caller calls free().
*/
// recursive solution 递归实现
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
if (root == NULL) {
*returnSize = 0;
return NULL;
}
//左子树
int returnSizeLeft = 0;
int *left = NULL;
if(root->left != NULL){
left= inorderTraversal(root->left, &returnSizeLeft);
}
//根结点
//右子树
int returnSizeRight = 0;
int *right = NULL;
if(root->right!= NULL){
right = inorderTraversal(root->right, &returnSizeRight);
}
*returnSize = returnSizeLeft + returnSizeRight + 1;
int* traversalResult=(int*)malloc((*returnSize)*sizeof(int));
int index = 0;
for (int i =0; i<returnSizeLeft; i++) {
traversalResult[index++] = left[i];
}
free(left);
traversalResult[index++] = root->val;
for (int i =0; i<returnSizeRight; i++) {
traversalResult[index++] = right[i];
}
free(right);
return traversalResult;
}
// iteratively solution 迭代实现
//迭代算法 iteratively
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
struct TreeNode** traversalResult=(struct TreeNode**)malloc(1000*sizeof(struct TreeNode*));
if (root == NULL) {
*returnSize = 0;
return NULL;
}
int *result=(int*)malloc(1000*sizeof(int));
*returnSize = 0;
int index = 0;
struct TreeNode* p = root;
while (p != NULL || index>0) {
printf("%d",index);
while (p != NULL) {
traversalResult[index++] = p;
p = p->left;
}
if (index >= 1) {
p = traversalResult[--index];
result[(*returnSize )++] = p->val;
p = p->right;
}
}
return result;
}
144. Binary Tree Preorder Traversal
Difficulty: Medium
Given a binary tree, return the preorder traversal of its nodes’ values.
Example:
**Input:** `[1,null,2,3]`
1
\
2
/
3
**Output:** `[1,2,3]`
Follow up: Recursive solution is trivial, could you do it iteratively?
Solution
Language: C
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Return an array of size *returnSize.
* Note: The returned array must be malloced, assume caller calls free().
*/
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
}
//iteratively solution 迭代解决
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
if (!root) {
*returnSize = 0;
return NULL;
}
int * result = (int *)malloc(sizeof(int) * (1000));
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * (1000));
struct TreeNode* p=root;
*returnSize = 0;
int stackIndex = 0;
while (p || stackIndex > 1) {
result[(*returnSize)++] = p->val;
if (p->right) {
stack[stackIndex++]=p->right;
}
p = p->left;
if (stackIndex > 0&&!p) {
p = stack[--stackIndex];
}
}
return result;
}
//recursive solution 递归解决
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
if (!root) {
* returnSize = 0;
return NULL;
}
//左节点
int leftSize = 0;
int *left = NULL;
if(root->left){
left = preorderTraversal(root->left, &leftSize);
}
//右节点
int rightSize = 0;
int *right = NULL;
if(root->right){
right = preorderTraversal(root->right, &rightSize);
}
*returnSize = leftSize + rightSize + 1;
int * result = (int *)malloc(sizeof(int) * (*returnSize));
int index = 0;
//根节点
result[index++] = root->val;
//左节点
for (int i =0; i<leftSize; i++) {
result[index++] = left[i];
}
free(left);
//右节点
for (int i =0; i<rightSize; i++) {
result[index++] = right[i];
}
free(right);
return result;
}
145. Binary Tree Postorder Traversal
Difficulty: Hard
Given a binary tree, return the postorder traversal of its nodes’ values.
Example:
**Input:** `[1,null,2,3]`
1
\
2
/
3
**Output:** `[3,2,1]`
Follow up: Recursive solution is trivial, could you do it iteratively?
Solution
Language: C
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Return an array of size *returnSize.
* Note: The returned array must be malloced, assume caller calls free().
*/
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
}
////迭代实现 iteratively solution
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
int *result = (int *)malloc(sizeof(int) * 1000);
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 1000);
* returnSize = 0;
int stackIndex = 0;
int *flag = (int *)malloc(sizeof(int) * 1000);//用来标记是否是第二次访问这个节点
struct TreeNode* p = root;
while (p || stackIndex > 1) {
if (p) {
int dex = stackIndex++;
stack[dex] = p;
flag[dex] = 1;
}
if (p->right) {
int dex = stackIndex++;
stack[dex] = p->right;
flag[dex] = 0;
}
p = p->left;
if (!p && stackIndex > 0) {
int loop =1;
while (loop && stackIndex>0) {
int index = --stackIndex;
p = stack[index];
if (flag[index] == 1) {
result[(*returnSize)++] = p->val;
loop = 1;
}
else{
loop =0;
}
}
if (stackIndex==0) {
return result ;
}
}
}
return result;
}
//递归实现 Recursive solution
int* postorderTraversal_1(struct TreeNode* root, int* returnSize) {
if (!root) {
*returnSize = 0;
return NULL;
}
int *left = NULL;
int leftSize = 0;
if (root->left) {
left = postorderTraversal(root->left, &leftSize);
}
int *right = NULL;
int rightSize = 0;
if (root->right) {
right = postorderTraversal(root->right, &rightSize);
}
*returnSize = leftSize + rightSize + 1;
int *result = (int *)malloc(sizeof(int) * (*returnSize));
int index = 0;
for (int i = 0; i < leftSize; i++) {
result[index++] = left[i];
}
for (int i = 0; i < rightSize; i++) {
result[index++] = right[i];
}
result[index] = root->val;
free(left);
free(right);
return result;
}
Review
Review单独作为一篇文章： https://dandan2009.github.io/2018/11/17/accelerating-your-coding-skills/
TIPS
这周把二叉树的相关概念整理一下
二叉树的一些相关概念:
二叉树（Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。 二叉树的第 i层至多拥有 2^i-1 个节点
与普通树不同 普通树的节点个数至少为1，而二叉树的节点个数可以为0； 普通树节点的最大分支度没有限制，而二叉树节点的最大分支度为2； 普通树的节点无左、右次序之分，而二叉树的节点有左、右次序之分。
二叉树通常作为数据结构应用，典型用法是对节点定义一个标记函数，将一些值与每个节点相关系。这样标记的二叉树就可以实现二叉搜索树和二叉堆，并应用于高效率的搜索和排序。
二叉树不是树的特例 尽管树和二叉树的概念之间有许多的类似，但它们是两个不同的数据结构。 因为从定义来看： 二叉树既不是只有两个子树的树，也不是最多只有两个子树的树。 树和二叉树最主要的区别是：二叉树中结点的子树要区分左子树和右字树，即使在结点只有一棵子树的情况下也要明确指出该子树是左子树还是右子树. 而树, 不管是有几颗子树的树, 各个子树地位都是一样的, 不像二叉树那样区分左右
二叉树是一种特殊的有序树：每个节点至多有两个分支（子节点），分支具有左右次序，不能颠倒。
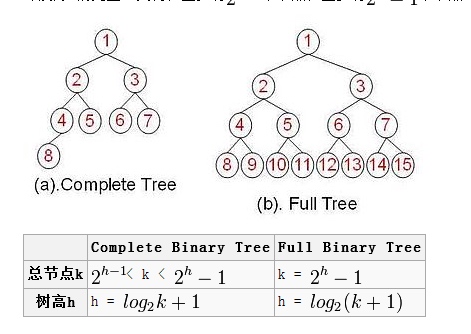
两种特殊的二叉树：
完全二叉树：除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点（注意是右边，而不能是左边缺少）。
满二叉树：每一层都是满的（除了最后一层，这里的最后一层是指叶节点）。
二叉树可以用数组或链接串列来存储，若是满二叉树就能紧凑排列而不浪费空间。如果某个节点的索引为i，（假设根节点的索引为0）则在它左子节点的索引会是 2i+1，以及右子节点会是 2i+2；而它的父节点（如果有）索引则为$\frac{i-1}{2}$。这种方法更有利于紧凑存储和更好的访问的局部性，特别是在前序遍历中。然而，它需要连续的存储空间，这样在存储高度为h的n个节点所组成的一般树时，将浪费很多空间。在最糟糕的情况下，如果深度为h的二叉树其每个节点都只有右孩子，则该存储结构需要占用 2^h - 1的空间，实际上却有h个节点，浪费了不少空间，是顺序存储结构的一大缺点。
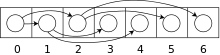一个存储在数组中的完全二叉树
深度优先遍历 在深度优先级中，我们希望从根结点访问最远的结点。和图的深度优先搜索不同的是，不需记住访问过的每一个结点，因为树中不会有环。前序，中序和后序遍历都是深度优先遍历的特例。参见深度优先搜索。
广度优先遍历 和深度优先遍历不同，广度优先遍历会先访问离根节点最近的节点。参见广度优先搜索。 二叉树的广度优先遍历又称按层次遍历。算法借助队列实现。
二叉树 定义：二叉树(binary tree)t是有限个元素的集合（可以为空）。当二叉树非空时，其中有一个称为根的元素，余下的元素（如果有的话）被组成2个二叉树，分别称为t的左子树和右子树。
二叉树和树的根本区别是：
二叉树可以为空，树不能为空 二叉树中每个元素都恰好有两棵子树（其中一个或两个可能为空）。而树中每个元素可以有若干子树。 在二叉树中每个元素的子树都是有序的，也就是说，可以用左、右子树来区别。而树的子树间是无序的。 下图给出了表示数学表达式的二叉树，总共有3个数学表达式。每个操作符可以有一个或两个操作数，左操作数是操作符的左子树，而右操作数则是右子树。树中的叶节点是常量或者变量。
二叉树的特性 特性1： 包含n(n>0)个元素的二叉树边数是n-1。
证明 二叉树中每个元素 (除了根节点)有且只有一个父节点。在子节点与父节点间有且只有一条边，因此边数为n-1。
二叉树的高度或者深度是指该二叉树的层数。
特性2： 若二叉树的高度为h,h≥0,则该二叉树最少有h个元素，最多有2h−1个元素。
证明 因为每一层最少要有1个元素，因此元素数最少为h。每元素最多有2个子节点，则第i层节点元素最多为2i−1个,i>0。h=0时，元素的总数为0，也就是20−1。当h>0时，元素的总数不会超过∑hi=12i−1=2h−1。
特性3： 包含n个元素的二叉树的高度最大是n，最小是⌈log2(n+1)⌉。
证明 因为每层至少有一个元素，因此高度不会超过n。由特性2，可以得知高度为h的二叉树最多有2h−1个元素。因为n≤2h−1,因此h≥log2(n+1)。由于h是整数，所以h≥⌈log2(n+1)⌉。
当高度是h的二叉树恰好有2h−1个元素时，称其为满二叉树(full binary tree)。下图就是一个高度为4的满二叉树。
假设对高度为h的满二叉树中的元素从上到下，从左到右的顺序进行从1到2h−1进行编号，如上图所示。假设从满二叉树中删除k个元素，其编号为2h−i,1≤i≤k,所得到的二叉树称为完全二叉树(complete binary tree)。如下图给出的三棵完全二叉树。注意，满二叉树是完全二叉树的一个特例，并且有n个元素的完全二叉树的深度是⌈log2(n+1)⌉。
在完全二叉树中，一个元素与其孩子的编号有非常好的对应关系。其关系在下面特性4中给出。
特性4： 设完全二叉树中一元素的序号是i，1≤i≤n。则有以下关系成立： 1) 当i=1时，该元素为二叉树的根，若i>1,则该元素父节点的编号是⌊i/2⌋。 2) 当2i>n时，该元素没有左子树，否则，其左子树的编号是2i。 3) 若2i+1>n时，该元素没有右子树，否则，其右子树的编号是2i+1。
二叉树
1.二叉树的基本形态：
二叉树也是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态：
(1)空二叉树 (2)只有一个根结点的二叉树 (3)只有右子树 (4)只有左子树 (5)完全二叉树
注意：尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。
2.两个重要的概念：
(1)完全二叉树——只有最下面的两层结点度小于2，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树； (2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶结点都处在最底层的二叉树,。
3.二叉树的性质 (1) 在二叉树中，第i层的结点总数不超过2^(i-1)； (2) 深度为h的二叉树最多有2^h-1个结点(h>=1)，最少有h个结点； (3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2， 则N0=N2+1； (4) 具有n个结点的完全二叉树的深度为int（log2n）+1 (5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系： 若I为结点编号则 如果I<>1，则其父结点的编号为I/2； 如果2I<=N，则其左儿子（即左子树的根结点）的编号为2I；若2I>N，则无左儿子； 如果2I+1<=N，则其右儿子的结点编号为2I+1；若2I+1>N，则无右儿子。 (6)给定N个节点，能构成h(N)种不同的二叉树。 h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1)。
满二叉树 一棵深度为k，且有2的(k)次方－1个节点的二叉树 特点：每一层上的结点数都是最大结点数
完全二叉树的定义：深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时，称为完全二叉树。 特点：叶子结点只可能在层次最大的两层上出现；对任一结点，若其右分支下子孙的最大层次为l，则其左分支下子孙的最大层次必为l 或l+1 满二叉树：一棵深度为k，且有2的(k)次方－1个节点的二叉树 特点：每一层上的结点数都是最大结点数 满二叉树肯定是完全二叉树完全二叉树不一定是满二叉树
但是二叉搜索树有个很麻烦的问题，如果树中插入的是随机数据，则执行效果很好，但如果插入的是有序或者逆序的数据，那么二叉搜索树的执行速度就变得很慢。因为当插入数值有序时，二叉树就是非平衡的了，它的快速查找、插入和删除指定数据项的能力就丧失了。
为了解决这个问题，我们可以使用多叉树。
2-3-4树就是一个多叉树，它的每个节点最多有四个子节点和三个数据项。2-3-4树和红-黑树一样，也是平衡树，它的效率比红-黑树稍差，但是编程容易。2-3-4树名字中的2、3、4的含义是指一个节点可能含有的子节点的个数。对非叶节点有三种可能的情况：
有一个数据项的节点总是有两个子节点； 有两个数据项的节点总是有三个子节点； 有三个数据项的节点总是有四个字节点。
二叉搜索树、2-3-4树、红-黑树
二叉树
参考; https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91 https://www.cnblogs.com/myjavascript/articles/4092746.html
Share
如何学习数据结构与算法？ 这个之前分享多一次，最近又看到一篇文章，和我的想法很吻合，这里再整理一下：
在刷题之前需要的基础 1、常见数据结构：链表、树(如二叉树)。 2、常见算法思想：贪婪法、分治法、穷举法、动态规划，回溯法。 3、常见的排序算法
如果你连这些最基本的都不知道的话，那么你再刷题的过程中，会很难受的，思路也会相对比较少，可以说很多题你只会使用暴力法，所以在刷题之前这些基本的东西还是要熟练掌握的，
还有一定要看书，进行系统的学习。
最后一个一定要多练，练习的过程要学习别人的优秀解法，不要自己做出来就万事大吉了，要看看别人的实现，自己认真分析一下。
刷题网站除了leetcode还有牛客网，以及下面的 18 个锻炼编程技能的网站 https://blog.csdn.net/lyn167/article/details/52134859 [topcoder] https://www.topcoder.com/ HackerEarth http://www.hackerearth.com/ Coderbyte https://coderbyte.com/ Project Euler : https://projecteuler.net/
参考： 我是如何学习数据结构与算法的？：https://mp.weixin.qq.com/s/Mo8xSmCnKrfIt3UpOLH6EQ 微信的内容经常丢失，这里复制一份：原文链接：https://mp.weixin.qq.com/s/Mo8xSmCnKrfIt3UpOLH6EQ
数据结构与算法的地位对于一个程序员来说不言而喻。今天这篇文章不是来劝你们学习数据结构与算法的，也不是来和你们说数据结构与算法有多重要。
主要是最近几天后台有读者问我是如何学习数据结构与算法的，有没有什么捷径，是要看视频还是看书，去哪刷题等…..而且有些还是大三大四的，搞的我都替你们着急、担心…..
所以我今天就分享下自己平时都是怎么学习的。
学习算法的捷径就是多刷题 说实话，要说捷径，我觉得就是脚踏实地着多动手去刷题，多刷题。
但是，如果你是小白，也就是说，你连常见的数据结构，如链表、树以及常见的算法思想，如递归、枚举、动态规划这些都没学过，那么，我不建议你去刷题的。而是先去找本书先去学习这些，然后再去刷题。
也就是说，假如你要去诸如leetcode这些网站刷题，那么，你要先具备一定的基础，这些基础包括：
1、常见数据结构：链表、树(如二叉树)。
2、常见算法思想：贪婪法、分治法、穷举法、动态规划，回溯法。
以上列出来的算是最基本的吧。就是说你刷题之前，要把这些过一遍再去刷题。如果你连这些最基本的都不知道的话，那么你再刷题的过程中，会很难受的，思路也会相对比较少。
总之，千万不要急，先把这些基本的过一遍，力求理解，再去刷题。这些基础的数据结构与算法，我是在大一第二学期学的，我没看视频，我是通过看书学的，那时候看的书是：
1、算法分析与分析基础：这本比较简单，推荐新手看。
2、数据结构与算法分析—-C语言描述：代码用C写的，推荐看。
3、挑战程序设计竞赛(第二版)：也是很不错的一本书，推荐看。
具体可以看我的另外一篇文章，里面是介绍这几本书的： 算法与数据结构书籍与视频福利
说实话，我那一学期的时间几乎都花在数据结构与算法上，但刷的题很少，只是书本上的一些例题。所以当我把这些基本的过一遍之后，再去一些网站刷题依旧非常菜。
所以你们千万别指望以为自己把这些思想学完之后刷题会很牛，只有多刷题，只有多动手实践，你的灵敏度才会提高起来。
在这里说一下前阵子有个非常火爆的专栏—-【数据结构与算法之美】
我没买这个专栏，我想说的是，买了就一定要去看，千万别浪费。也千万不要觉得学完这个专栏你就会变的多牛逼，如果你只是跟着进度去学习这个专栏，自己没有花时间去刷题、去动手时间。那我可以保证，你学完之后还是那么菜。
总结下：
提高数据结构与算法没啥捷径，最好的捷径就是多刷题。但是，刷题的前提是你要先学会一些基本的数据结构与算法思想。
追求完美 如何刷题？如何对待一道算法题？
我觉得，在做题的时候，一定要追求完美，千万不要把一道题做出来之后，提交通过，然后就赶紧下一道。
算法能力的提升和做题的数量是有一定的关系，但并不是线性关系。也就是说，在做题的时候，要力求一题多解，如果自己实在想不出来其他办法了，可以去看看别人是怎么做的，千万不要觉得模仿别人的做法是件丢人的事。
我做题的时候，我一看到一道题，可能第一想法就是用很粗糙的方式做，因为很多题采用暴力法都会很容易做，就是时间复杂度很高。之后，我就会慢慢思考，看看有没其他方法来降低时间复杂度或空间复杂度。最后，我会去看一下别人的做法，当然，并不是每道题都会这样执行。
衡量一道算法题的好坏无非就是时间复杂度和空间复杂度，所以我们要力求完美，就要把这两个降到最低，令他们相辅相成。
我举道例题吧：
问题： 一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法？
这道题我在以前的分章分析过，不懂的可以先看下之前写的：递归与动态规划—基础篇1
方法1：：暴力递归
这道题不难，或许你会采取下面的做法：
public static int solve(int n){ if(n == 1 || n == 2){ return n; }else if(n <= 0){ return 0; }else{ return solve(n-1) + solve(n-2); } }
这种做法的时间复杂度很高，指数级别了。但是如果你提交之后侥幸通过了，然后你就接着下一道题了，那么你就要好好想想了。
方法二：空间换时间
力求完美，我们可以考虑用空间换时间：这道题如何你去仔细想一想，会发现有很多是重复执行了。所以可以采取下面的方法：
//用一个HashMap来保存已经计算过的状态 static Map<Integer,Integer> map = new HashMap(); public static int solve(int n){ if(n <= 0)return 0; else if(n <= 2){ return n; }else{//是否计算过 if(map.containsKey(n)){ return map.get(n); }else{ int m = solve(n-1) + solve(n-2); map.put(n, m); return m; } } }
这样，可以大大缩短时间。也就是说，当一道题你做了之后，发现时间复杂度很高，那么可以考虑下，是否有更好的方法，是否可以用空间换时间。
方法三：斐波那契数列
实际上，我们可以把空间复杂度弄的更小，不需要HashMap来保存状态：
public static int solve(int n){ if(n <= 0) return 0; if(n <= 2){ return n; }
int f1 = 0; int f2 = 1; int sum = 0; for(int i = 1; i<= n; i++){ sum = f1 + f2; f1 = f2; f2 = sum; } return sum; }
我弄这道题给你们看，并不是在教你们这道题怎么做，而是有以下目的：
1、在刷题的时候，我们要力求完美。
2、我想不到这些方法啊，怎么办？那么你就可以去看别人的做法，之后，遇到类似的题，你就会更有思路，更知道往哪个方向想。
3、可以从简单暴力入手做一道题，在考虑空间与时间之间的衡量，一点点去优化。
推荐一些刷题网站 我一般是在leetcode和牛客网刷题，感觉挺不错，题目难度不是很大。
在牛客网那里，我主要刷剑指Offer,不过那里也有个在线刷leetcode，不过里面的题量比较少。牛客网刷题有个非常方便的地方就是有个讨论区，那里会有很多大佬分享他们的解题方法，不用我们去百度找题解。所以你做完后，实在想不出，可以很方便着去看别人是怎么做的。
至于leetcode，也是大部分题目官方都有给出答案，也是个不错的刷题网站。你们可以两个挑选一个，或者两个都刷。
当然，还有其他刷题的网站，不过，其他网站没刷过，不大清除如何。
再说数据结构 前面我主要是说了我平时都是怎么学习算法的。在数据结构方法，我只是列举了你们一定要学习链表和树(二叉堆)，但这是最基本的，刷题之前要掌握的，对于数据结构，我列举下一些比较重要的：
1、链表（如单向链表、双向链表）。
2、树（如二叉树、平衡树、红黑树）。
3、图（如最短路径的几种算法）。
4、队列、栈、矩阵。
对于这些，自己一定要动手实现一遍。你可以看书，也可以看视频，新手可以先看视频，不过前期可以看视频，之后我建议是一定要看书。
视频和书我以前有推荐过： 算法与数据结构书籍与视频福利
例如对于平衡树，可能你跟着书本的代码实现之后，过阵子你就忘记，不过这不要紧，虽然你忘记了，但是如果你之前用代码实现过，理解过，那么当你再次看到的时候，会很快就记起来，很快就知道思路,而且你的抽象能力等等会在不知不觉中提升起来。之后再学习红黑树啊，什么数据结构啊，都会学的很快。
最最重要 动手去做，动手去做，动手去做。重要的话说三遍。
千万不要找了一堆资源，订好了学习计划，我要留到某某天就来去做…..
千万不要这样，而是当你激情来的时候，就马上去干，千万不要留到某个放假日啊什么鬼了，很多这种想法的人，最后会啥也没做的。
也不要觉得要学习的有好多啊，不知道从哪学习起。我上面说了，可以先学习最基本的，然后刷题，刷题是一个需要长期坚持的事情，一年，两年。在刷题的过程中，可以穿插学习其他数据结构。
